逻辑回归#
逻辑回归(Logistic Regression),虽然名字里有 “回归” 二字,但实际上是解决分类问题的一类线性模型。又被称作 logit 回归,maximum-entropy classification(MaxEnt,最大熵分类),或 log-linear classifier(对数线性分类器)。
逻辑回归它基于线性回归模型,通过一个非线性的逻辑函数(称为“sigmoid函数”或“逻辑函数”)将预测结果映射到概率值,从而对样本进行分类。数学模型如下:
\(hθ(x) = g(θ^T x)\) ,其中 \(g(z) = \frac{1}{1 + e^{-z}} \) 是逻辑函数。
sigmoid函数#
函数表达式为:
\( f(x) = \frac{1}{1 + e^{-x}} \)
我们用代码将这个函数绘制出来:
import numpy as np
import matplotlib.pyplot as plt
def sigmoid(x):
return 1 / (1 + np.exp(-x))
# 生成一系列x值
x = np.linspace(-10, 10, 100)
# 计算对应的sigmoid值
y = sigmoid(x)
# 绘制sigmoid函数曲线
plt.plot(x, y)
plt.xlabel('x')
plt.ylabel('sigmoid(x)')
plt.title('Sigmoid Function')
plt.grid(True)
plt.show()
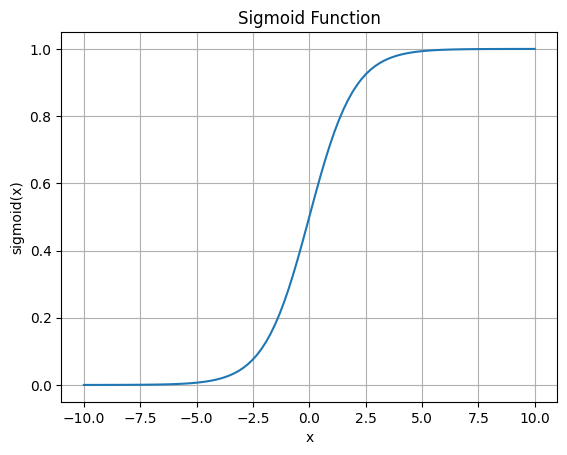
这个函数图像看着就很对称,也很优雅。记为\(f(x) = \frac{1}{1 + e^{-x}}\)
对这个函数求导为:
\(f’(x) = \frac{d}{dx} \left(\frac{1}{1 + e^{-x}}\right)\)
进一步可以得到(推导略)
\(f’(x) = 2f(x)(1 - f(x))\)
换句话说,sigmoid函数的导数值,仅仅依靠该函数值本身的四则运算就可以计算得到,计算可谓是非常简便。
损失函数(Loss Function):#
参考[1]
我们知道一个样本最终的计算值在 \((0,1)\) 之间浮动,可以被视作概率值。并且由于sigmoid函数的单调性,我们可以认为,概率值越接近1,说明样本越接近正样本,评价质量越好
因此,我们可以构造一个似然函数,它衡量了计算得分值和真实样本标签之间的差距,当样本只有一个的时候:
\(L(w) = (p(x))^y (1-p(x))^{(1-y)}\)
当样本有N个的时候
\(L(w) = \prod_{i=0}^{n} (p(x_i))^y_i (1-p(x_i))^{(1-y_i)}\)
再考虑到该函数的连乘,也未对样本的数量做归一化,应当转换成
\(J(w) = -\frac{1}{N} \ln L(w)\)
加上L2正则化项为:
\( J(w) = -\frac{1}{N} \ln L(w) + \frac{\lambda}{2N}\sum_{j=1}^{m} w_j^2 \)
其中,\(J(w)\) 是目标函数,\(w\) 是模型的参数向量,\(N\) 是训练样本数量,\(w_j\) 是第 \(j\) 个特征的权重,\(λ\) 是正则化参数,\(m\) 是参数个数。
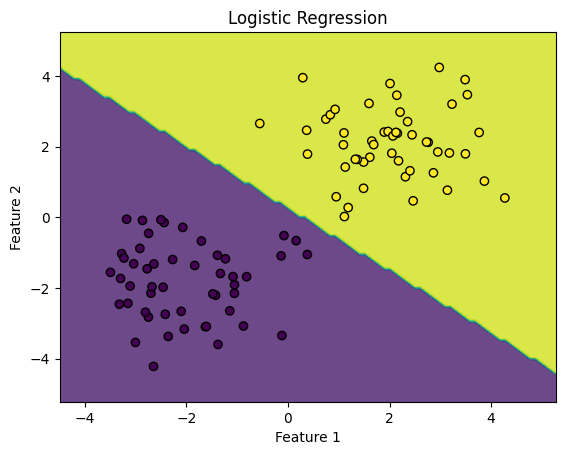
下面演示一个逻辑回归分类的示例:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LogisticRegression
# 创建一些随机数据用于训练
np.random.seed(0)
X1 = np.random.randn(50, 2) + [2, 2]
X2 = np.random.randn(50, 2) + [-2, -2]
X = np.concatenate((X1, X2))
y = np.concatenate((np.ones(50), np.zeros(50)))
# 训练逻辑回归模型
model = LogisticRegression()
model.fit(X, y)
# 可视化分类结果
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.linspace(x_min, x_max, 100), np.linspace(y_min, y_max, 100))
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, alpha=0.8)
plt.scatter(X[:, 0], X[:, 1], c=y, edgecolors='k')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.title('Logistic Regression')
plt.show()