决策树#
假设我们有一个数据集包含鸢尾花的特征(萼片长度、萼片宽度、花瓣长度和花瓣宽度)以及对应的类别(Setosa、Versicolor、Virginica)。最简单的决策树就是个if-else-then的分支。例如对鸢尾花数据分类可以这样做。
import numpy as np
def predict(features):
# 决策树的判定条件和结果
if features[2] <= 2.45:
return 'setosa'
elif features[3] <= 1.75:
if features[2] <= 4.95:
if features[3] <= 1.65:
return 'versicolor'
else:
return 'virginica'
else:
if features[3] <= 1.55:
return 'virginica'
else:
return 'versicolor'
else:
return 'virginica'
# 测试样例
X_test = np.array([[5.1, 3.5, 1.4, 0.2],
[6.3, 2.9, 5.6, 1.8],
[4.9, 3.0, 1.4, 0.2]])
for i in range(len(X_test)):
prediction = predict(X_test[i])
print("Sample", i+1, "prediction:", prediction)
Sample 1 prediction: setosa
Sample 2 prediction: virginica
Sample 3 prediction: setosa
决策树算法流程#
将这个经验法则通过数学和算法的方式来自动化处理,就衍生了很多决策树算法。以鸢尾花分类为例,这些算法基本上是这样的过程:
特征选择:从训练数据集中选择最优特征作为当前节点的划分特征。通常使用某种准则(如信息增益、基尼指数或信息增益比)来评估特征的重要性。
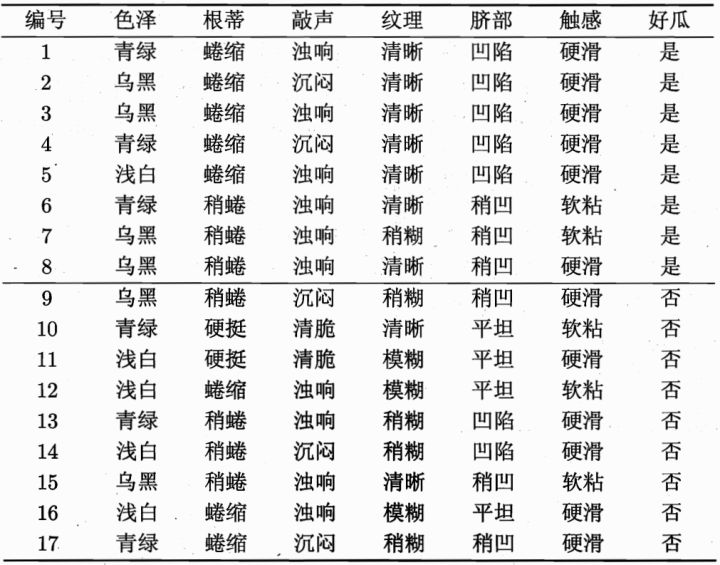
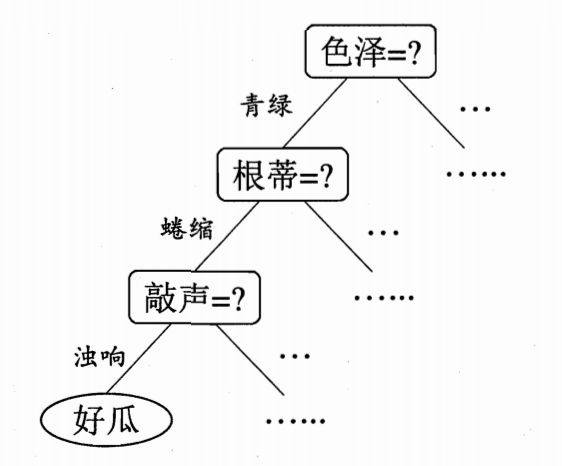
树节点划分:根据选择的特征将训练数据集划分成子集。对于分类问题,每个子集对应于一个特征值或特征值范围;对于回归问题,则根据特征的阈值进行划分。
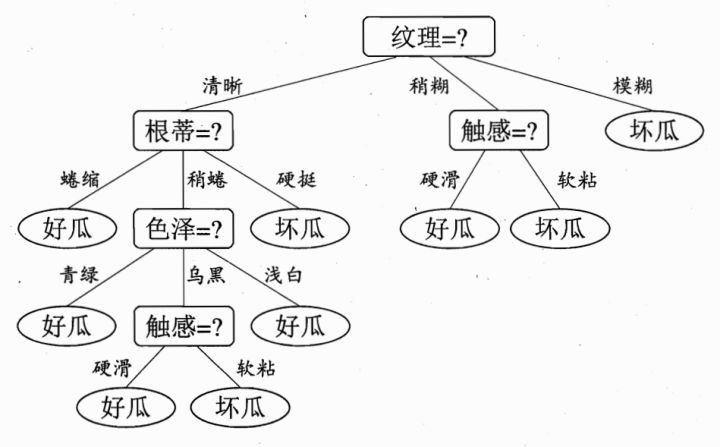
递归构建子树:对每个子集递归地应用上述步骤,构建决策树的子树。如果子集中的样本属于同一类别(或具有相似的回归值),则停止划分。
第一层
根节点:被分成17份,8是%2F9否,总体的信息熵为:
\( H_0 = - p(是) * log_2(p(是)) - p(否) * log_2(p(否)) = - 0.471 * log2(0.471) - 0.529 * log2(0.529) ≈ 0.998 \)
第二层
清晰:被分成9份,7是/2否,它的信息熵为:
\(H_1 = - 7 / 9 * log2(7 / 9) - 2 / 9 * log2(2 / 9) = 0.764\)
稍糊:被分成5份,1是/4否,它的信息熵为:
\(H_2 = - 1 / 5 * log2(4 / 5) - 1 / 5 * log2(4 / 5) = 0.722\)
模糊:被分成3份,0是/3否,它的信息熵为:
\(H_3 = 0\)
假设我们选取纹理为分类依据,把它作为根节点,那么第二层的加权信息熵可以定义为:
\(H’ = 9/17 * H_1 + 5/17 * H_2 + 3/17 * H_3 \)
因为\(H’< H\),也就是随着决策的进行,其不确定度要减小才行,决策肯定是一个由不确定到确定状态的转变。
剪枝:对生成的决策树进行剪枝操作,以减小过拟合风险。剪枝方法可以是预剪枝(在构建树时提前停止划分)或后剪枝(在完整构建树之后剪掉部分叶节点)。
终止条件:根据停止条件,确定是否继续构建子树。常见的停止条件包括达到最大深度、样本数量不足或没有更多特征可用。
输出决策树:得到最终的决策树模型,可以将其用于预测新的输入数据。
对于集成学习算法(如随机森林和GBDT),会有一些额外步骤:
集成学习:对多个决策树进行集成。对于随机森林,每个决策树通过自助采样从原始训练数据集中获得;对于GBDT,每个决策树都是基于前一棵树的残差进行训练。
预测结果:对于分类问题,通过投票或多数表决来确定最终的类别;对于回归问题,则取平均或加权平均作为最终的预测值。
常见决策树算法#
信息熵(information entropy)是信息论的基本概念。描述信息源各可能事件发生的不确定性。20世纪40年代,香农(C.E.Shannon)借鉴了热力学的概念,把信息中排除了冗余后的平均信息量称为“信息熵”,并给出了计算信息熵的数学表达式。信息熵的提出解决了对信息的量化度量问题[1]。
设有一个分类问题的训练数据集S,其中包含C个类别。对于每个类别c,假设样本属于该类别的概率为p©。则数据集S的信息熵定义如下:
\( H = \text{Entropy}(S) = -\sum_{c=1}^{C} p(c) \log_{2}(p(c)) \)
其中,对数函数可以选择任意基数(通常选择2作为基数),p©表示样本属于类别c的概率。
以下是计算信息熵的简单示例:
\(S = \{ A, A, A, B, B, C \} \)
\( p(A) = 3/6 = 0.5 \\ p(B) = 2/6 ≈ 0.333 \\ p(C) = 1/6 ≈ 0.167 \)
\( H = Entropy(S) \\ = -(0.5 * log_2(0.5) + 0.333 * log_2(0.333) + 0.167 * log_2(0.167)) \\ ≈ -(0.5 * (-1) + 0.333 * (-1.585) + 0.167 * (-2)) \\ ≈ 1.459 \\ \)
因此,该数据集的信息熵约为1.459。
通过计算信息熵,我们可以衡量数据集中样本的不确定性程度。在决策树算法中,我们希望选择具有最低信息熵(或最大信息增益)的特征来进行划分,以使得子集的不确定性减少,并提高决策树模型的预测能力。
越高 = 越混乱 = 越不纯 = 越不确定
import numpy as np
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
from sklearn import tree
import matplotlib.pyplot as plt
# 加载鸢尾花数据集
iris = load_iris()
X = iris.data
y = iris.target
# 构建决策树模型
model = DecisionTreeClassifier()
model.fit(X, y)
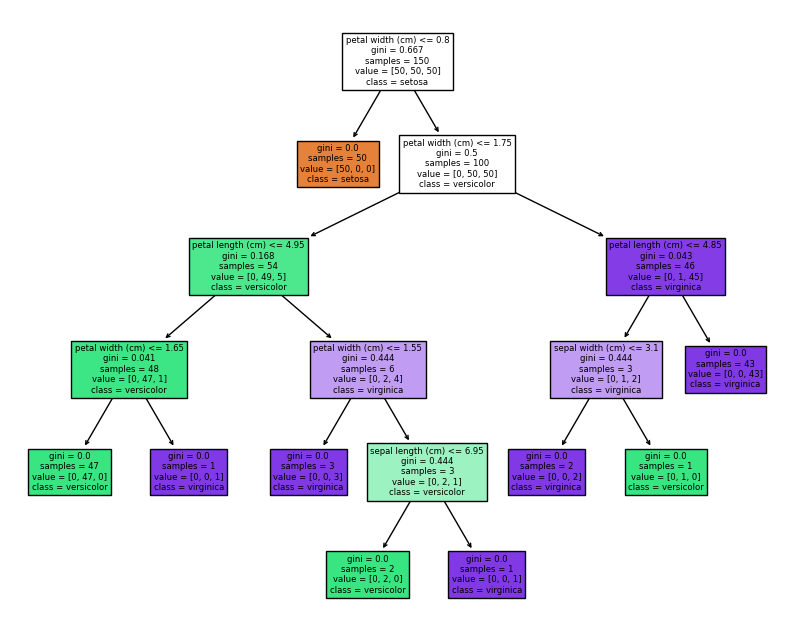
# 可视化决策树
fig = plt.figure(figsize=(10, 8))
_ = tree.plot_tree(model, feature_names=iris.feature_names, class_names=iris.target_names, filled=True)
plt.show()
ID3(Iterative Dichotomiser 3)#
使用信息增益作为特征选择准则来构建决策树。适用于离散型特征和多类别问题。
\(Gain(X, Y) = H(Y) - H(Y|X)\)
比如上面实例中我选择纹理作为根节点,将根节点一分为三,则:
\(Gain(X, 纹理) = 0.998 - 0.764 = 0.234\)
意思是,没有选择纹理特征前,是否是好瓜的信息熵为0.998,在我选择了纹理这一特征之后,信息熵下降为0.764,信息熵下降了0.234,也就是信息增益为0.234。
如果某个特征的信息增益较大,意味着使用该特征进行划分能够带来更多的信息量,因此该特征被认为是比较重要的。
C4.5#
C4.5是ID3算法的改进版,优化之一就是引入了信息增益率来解决ID3中信息增益偏向于具有更多取值的特征的问题。
信息增益率=信息增益/特征本身的熵:
\(Gain_{ratio}(X, Y) = \frac{Gain(X, Y}{H_Y(X)}\)
\(H_Y(X) = -\sum_{i=1}^{n}\frac{|X_i|}{|X|}\log_2\frac{|X_i|}{|X|}\)
信息增益率对可取值较少的特征有所偏好(分母越小,整体越大),因此C4.5并不是直接用增益率最大的特征进行划分,而是使用一个启发式方法:先从候选划分特征中找到信息增益高于平均值的特征,再从中选择增益率最高的。
CART(Classification and Regression Trees)#
使用基尼系数作为特征选择准则。基尼指数(基尼不纯度):表示在样本集合中一个随机选中的样本被分错的概率。 基尼系数越小,不纯度越低,特征越好。这和信息增益(率)正好相反。基尼指数可以用来度量任何不均匀分布,是介于0-1之间的数,0是完全相等,1是完全不相等。
\(Gini(D) = 1 - \sum_{k=1}^{K} (p_k)^2\)
ID3算法只能处理离散特征的分类问题,C4.5能够处理离散特征和连续特征的分类问题,CART算法可以处理离散和连续特征的分类与回归问题。
